Today in math class, we had a work period, so there’s not much to write about; so I thought I would make a review on everything we’ve learned up to this point.


Sept. 8 Quadratic Functions

Using the formula y-k = a (x-h) ², we can calculate:

i) Vertex - (h,k)
ii) Minimum/ Maximum - (depends on direction of opening), = k
iii) Axis of symmetry - x = h


Sept. 12 Quadratic Functions Cont’d
“The Parabola”

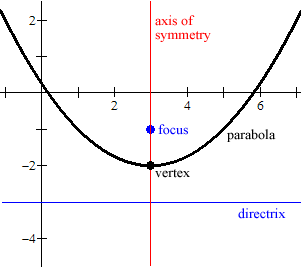
Characteristics of a Parabola
opening up or down is determined by the coefficient of the x² term
* a > 0 - opens up * a <>* a = 0 - not quadratic

y-k = a ( x – h ) ²
‘a’ --- gives the opening
‘x=h’- equation of axis of symmetry
‘h,k’ - ordered pair of vertex

Brackets
[ - up to and including
( - up to and not including



To sum up this blog, here is an example:

Ex) y = ( x + 2 ) ²
Vertex ------------------------------( -2,0)
Equation of axis of symmetry – x = 2
Domain –--------------------------- (-∞,∞)
Range------------------------------- [ 0, ∞)
X intercepts –---------------------- at -2
Direction of opening-------------- up
Max or Min------------------------- min @ 0


Tomorrow's scribe will be Jayde.

Here are some links that you can check out:
http://www.mathwords.com/p/parabola.htm
http://mathworld.wolfram.com/Parabola.html
http://www-groups.dcs.st-and.ac.uk/~history/Curves/Parabola.html